Diagonalisation des endomorphismes
Diagonalisation des endomorphismes
Soit 
un endomorphisme de 
dont la matrice dans la base canonique est :
Question
Calculer le polynôme caractéristique de 
. En déduire les valeurs propres de .
Le polynôme caractéristique est :
Donc :
Le polynôme caractéristique a trois racines : 
; 
;
.
Question
Montrer que admet une valeur propre double si et seulement si 
ou 
.
Trois cas sont possibles :
Si
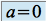alors a deux valeurs propres : de multiplicité 
, et 
de multiplicité ,Si
alors a deux valeurs propres : de multiplicité , et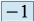 
de multiplicité ,Si
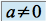et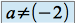 
alors a trois valeurs propres simples : ; ;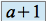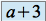. est donc diagonalisable.
Question
Préciser dans les deux cas précédents si est diagonalisable.
Dans les premiers deux cas, pour savoir si est diagonalisable, il suffit de vérifier que la dimension des espaces propres est égale à la multiplicité des valeurs propres dans le polynôme caractéristique.
Pour cela, il suffit de déterminer le rang de 
cas
:
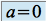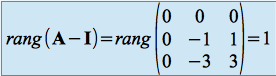
Donc
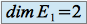. Et est égal à la multiplicité de la valeur propre . L'autre valeur propre étant simple, l'espace propre associé est de dimension . est donc diagonalisable.cas
:
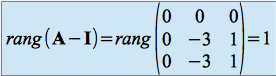
Donc
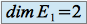. Et est égal à la multiplicité de la valeur propre . L'autre valeur propre étant simple, l'espace propre associé est de dimension . est donc diagonalisable.
Question
Dans le cas , déterminer une base de chaque espace propre.
Dans le deuxième cas, déterminons une base de chaque espace propre.
Pour 
:
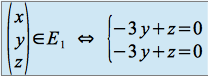
Donc 
Pour 
:
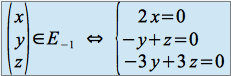
Une base de est donc :
