Diagonalisation des endomorphismes
Diagonalisation des endomorphismes
Soit 
la base canonique de 
Soit 
l'endomorphisme dont 
est la matrice dans la base .
Dans les trois cas suivants ,
est-il diagonalisable ?Si oui , déterminer une base
dans laquelle la matrice de est diagonale. Sinon peut-on trigonaliser ?Déterminer
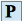la matrice de passage de à et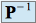 
la matrice de passage de à
Note : on peut obtenir une matrice triangulaire lorsque le polynôme caractéristique est scindé et que la dimension des espaces propres n'est pas égale à l'ordre de multiplicité des valeurs propres associées (on dit alors que l'on peut trigonaliser l'endomorphisme ).
Question
Le polynôme caractéristique de est :
Donc
a trois valeurs propres distinctes : 0,1 et 2. étant de dimension 3, on en déduit que est diagonalisable. Déterminons les espaces propres associés à chaque valeur propre (il s'agit de trois droites vectorielles) :
Pour 
, résolvons 
soit
donc 
Pour 
, résolvons 
soit 
donc 
Pour 
, résolvons 
soit 
donc 
avec : 
et 
Dans la base formée de vecteurs propres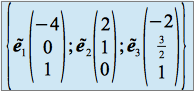 
la matrice de est : 
Question
Le polynôme caractéristique de est :
Donc
a deux valeurs propres distinctes. Déterminons les espaces propres :
Pour , résolvons soit
donc 
Pour 
, résolvons 
soit
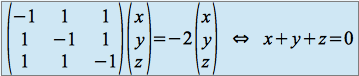
donc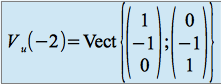 
La dimension des espaces propres est égale à l'ordre de multiplicité des valeurs propres donc est diagonalisable .
avec 
et 
Dans la base formée de vecteurs propres 
, la matrice est :
Question
Le polynôme caractéristique de est :
Donc
a deux valeurs propres distinctes. Déterminons les espaces propres :
Pour , résolvons soit
donc 
Pour , résolvons soit
donc 
La dimension des espaces propres n'est pas égale à l'ordre de multiplicité des valeurs propres donc est n'est pas diagonalisable.
Mais ayant un polynôme caractéristique scindé (c'est à dire factorisable en facteurs du premier degré) alors est trigonalisable. Complétons la famille de vecteurs propres pour avoir une base de par exemple par 
Déterminons l'écriture de dans la base 
il suffit d'écrire l'image de par dans cette base .
On cherche donc 
tels que
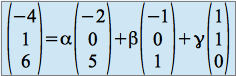
On trouve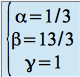 
Dans la base La matrice de s'écrit donc :
. Cette matrice est bien triangulaire.
