Matrice d'une application linéaire
Matrice d'une application linéaire
Soit ![]() une constante réelle et
une constante réelle et ![]() l'application de
l'application de ![]() , de base canonique
, de base canonique ![]() , dans
, dans ![]() , de base canonique
, de base canonique ![]() , définie par :
, définie par :
![]() .
.
Question
Montrer que, quel que soit le réel ![]() donné,
donné, ![]() est une application linéaire.
est une application linéaire.
Il faut prouver que quels que soient ![]() et
et ![]() , éléments de
, éléments de ![]() , et quel que soit le réel
, et quel que soit le réel ![]() :
:
![]() .
.
Il faut donc calculer ![]() .
.
Question
Ecrire la matrice ![]() de
de ![]() dans les bases canoniques de
dans les bases canoniques de ![]() et
et ![]() .
.
On exprime ![]() ,
, ![]() et
et ![]() dans la base canonique
dans la base canonique ![]() . On trouve :
. On trouve :
![]() .
.
Question
On définit dans
 les vecteurs :
les vecteurs :

Montrer que![]() est une base de
est une base de ![]() .
.
On définit dans
 les vecteurs
les vecteurs
![]()
Montrer que![]() est une base de
est une base de ![]() .
.
Ecrire la matrice
 de l'application
de l'application 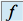 dans les bases
dans les bases 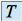 et
et 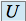 .
.
 est de dimension 3.
est de dimension 3. 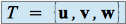 est donc une base de
est donc une base de  si et seulement si c'est une famille libre.
si et seulement si c'est une famille libre. est de dimension 2.
est de dimension 2.  est donc une base de
est donc une base de  si et seulement si c'est une famille libre.
si et seulement si c'est une famille libre.Il faut calculer les coordonnées de
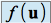 ,
, 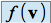 , et
, et  dans la base canonique de
dans la base canonique de  puis dans la base
puis dans la base  . On trouve :
. On trouve :
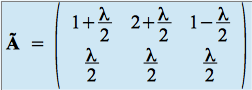 .
.





