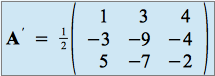Changement de bases
Changement de bases
Soit 
l'application linéaire de 
dans , définie par sa matrice dans la base canonique :
étant un endomorphisme, on prend la même base dans l'ensemble de départ et dans l'ensemble d'arrivée (puisque c'est le même ensemble).
On considère une nouvelle base :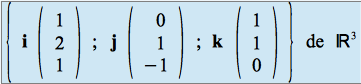 
Question
Calculer les images par des vecteurs 
et déterminer directement la matrice 
de dans cette nouvelle base. On dit que les matrices 
et sont équivalentes : elles représentent le même endomorphisme dans des bases différentes.
Calculer les coordonnées des images des vecteurs dans la base 
. On obtient ainsi les colonnes de la matrice cherchée.
Question
Retrouver le résultat du 1) en utilisant la formule de changement de base vue en cours.
Ici, dans la formule du cours, 
d'où : 
En remplaçant par les matrices, le calcul donne le résultat suivant :
