L'espace vectoriel des matrices à n lignes et p colonnes
Définition :
On note 
l'ensemble des matrices à coefficients dans le corps 
ayant 
lignes et 
colonnes.
Dans le cas où 
, on note 
, et on parle de matrices carrées d'ordre à coefficients dans .
Sur , on peut introduire les opérations suivantes :
La somme de deux matrices
et 
,
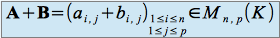la multiplication d'une matrice
par un scalaire 
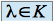, notée .,
.
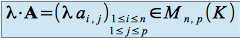Fondamental : Propriété
L'ensemble des matrices , muni de la somme des matrices et de la multiplication par un scalaire, 
, est un espace vectoriel sur de dimension 
.
Une base de cet espace, la base canonique par exemple, est formée des matrices notées 
dont dont le seul terme non nul et égal à 1 se trouve à l'intersection de la ligne 
et de la colonne 
.
Exemple :
Par exemple, une base de 
est constituée des matrices :
, 
, 
, 
, 
, 
.
