Introduction
Soient ![]() et deux espaces vectoriels sur le même corps
et deux espaces vectoriels sur le même corps ![]() , de dimensions finies respectives
, de dimensions finies respectives ![]() et
et ![]() . En ce qui concerne le corps de référence, on aura en général
. En ce qui concerne le corps de référence, on aura en général ![]() =
=![]() ou bien
ou bien ![]() =
=![]() .
.
Association d'une matrice à une application linéaire
A toute application linéaire ![]() de
de ![]() dans
dans ![]() , on peut associer une matrice, c'est à dire un tableau de scalaires dans le corps
, on peut associer une matrice, c'est à dire un tableau de scalaires dans le corps ![]() de référence, qui représente les actions élémentaires de l'application en question exprimées dans les bases particulières des espaces source et image (
de référence, qui représente les actions élémentaires de l'application en question exprimées dans les bases particulières des espaces source et image (![]() et
et ![]() ) de cette application.
) de cette application.
Représentation matricielle d'une application linéaire
En particulier, on peut représenter l'application linéaire ![]() de
de ![]() dans
dans ![]() par la matrice
par la matrice
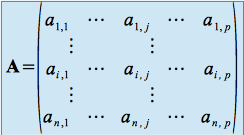
possédant ![]() lignes et
lignes et ![]() colonnes, dans laquelle les coefficients
colonnes, dans laquelle les coefficients ![]() correspondent, par exemple, aux composantes dans la base canonique
correspondent, par exemple, aux composantes dans la base canonique ![]() de
de ![]() , de l'image par
, de l'image par ![]() des vecteurs de la base canonique de
des vecteurs de la base canonique de ![]()
![]() .
.
Choix des bases
Le choix des bases influe bien évidemment directement sur la représentation matricielle d'une application linéaire, mais si on utilise les mêmes bases pour représenter diverses applications linéaires de ![]() dans
dans ![]() , on peut alors introduire certaines opérations sur ces matrices qui permettent de représenter directement sous forme matricielle les opérations équivalentes portant sur les applications linéaires
, on peut alors introduire certaines opérations sur ces matrices qui permettent de représenter directement sous forme matricielle les opérations équivalentes portant sur les applications linéaires ![]() dans
dans ![]() elles mêmes.
elles mêmes.





