Introduction to Data Assimilation for Scientists and Engineers

\(\displaystyle {d H(t)\over dt} = - \alpha \, H(t) + P(t)\) with \(H(0)= H_0\)

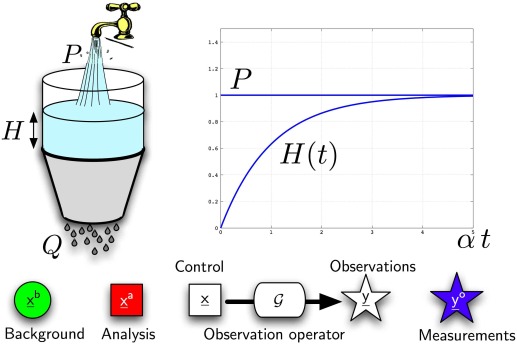
• Control space: \(\underline{x}=(\alpha, P)\)

• Measurments: \(\underline{y}^o=(H^o_1, ..., H^o_i, ..., H^o_M)\) with \(H^o_i=H^o(t_i)\)

• Observation operator: \({\cal G}(\alpha, P) = ({\cal G}_1, ..., {\cal G}_i, ..., {\cal G}_M)\) with \({\cal G}_i(\alpha, P) = H_i\)

• Observation errors: \(\underline{\underline R} =\hbox{diag}\,(\sigma_1^2, ..., \sigma_i^2, ..., \sigma_M^2)\)

• Background errors: \(\displaystyle\underline{\underline B} = \left(\begin{matrix}\sigma_{\alpha}^2 & \rho\, \sigma_{\alpha} \, \sigma_{P}\cr\rho\, \sigma_{\alpha} \, \sigma_{P} & \sigma_{P}^2\end{matrix}\right)\) with \(\displaystyle \rho ={ \left< \alpha' \, P' \right> \over\sigma_{\alpha} \, \sigma_{P}}\)