Introduction to Data Assimilation for Scientists and Engineers

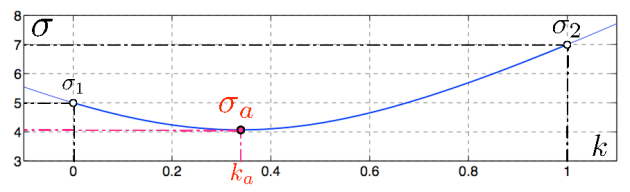
Searching the analysis in the form \(T_a = (1-k) \, T_1 + k \, T_2\)

Independent measurements: \(\left< T_1'\, T_2' \right> = 0\quad \Longrightarrow \quad \sigma_a^2 = (1-k)^2 \, \sigma_1^2 + k^2 \, \sigma_2^2\)

The analysis variance is minimum for \(\displaystyle ~~~{\color{red} k_a} = {\sigma_2^{-2}\over \sigma_1^{-2} + \sigma_2^{-2}}~~~\) and reads \(\displaystyle ~~~{\color{red} \sigma_a^2} = \left(\sigma_1^{-2} + \sigma_2^{-2}\right)^{-1}\)

Therefore : \(\displaystyle {\color{red} T_a ={C_1 \, T_1 + C_2 \, T_2 \over C_1 + C_2}}\) with \(\displaystyle C_1 ={ 1\over\sigma_1^{2}}\), \(\displaystyle ~~~ C_2 = {1\over \sigma_2^{2}}\) and \(\displaystyle ~~~ {\color{red}C_a}= {1\over \sigma_a^{2}} = C_1 + C_2\)