Les cellules photovoltaïques [La jonction PN et ses applications]

Les cellules photovoltaïques

Là encore il s'agit d'une jonction PN.

La cellule photovoltaïque est caractérisée par son courant électromoteur et sa force électromotrice.

Définition :

Le courant électromoteur est le courant de court-circuit $I_{CC}$ .

La force électromotrice est la tension de circuit ouvert $V_{CO}$ .

Ils sont donnés par :

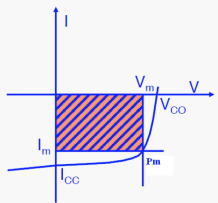
I_{CC} = I_{ph} et V_{CO} = \frac{k T}{q} Ln (\frac{I_{ph}}{I_{s}} + 1)

Définition : Puissance débitée

La puissance fournie par la photopile est donnée par le produit $V I$ :

P = V I = V {I_{ph} - I_{s} [\exp (\frac{q V}{kT}) - 1]}

Cette puissance est maximale au point $P_{m}$ défini par $dP / dV = 0$ , soit :

I_{ph} - I_{s} [\exp (\frac{q V}{kT}) - 1] - I_{s} \frac{q V}{kT} \exp (\frac{q V}{kT}) = 0.

La tension $V_{m}$ et le courant $I_{m}$ au point $P_{m}$ sont donnés par : $(1 + \frac{q V_{m}}{kT}) \exp (\frac{q V_{m}}{kT}) = 1 + \frac{I_{ph}}{I_{s}}$ .

I_{m} = I_{s} \frac{q V_{m}}{kT} \exp (\frac{q V_{m}}{kT})

La puissance débitée est alors donnée par le produit $V_{m} I_{m}$ (zone hachurée) qui s'écrit :

Définition :

P_{m} = V_{m} I_{m} = FF V_{CO} I_{CC}

Cette valeur est de l'ordre de 80% du produit $V_{CO} I_{CC}$ .

Le paramètre $FF$ est le facteur de remplissage ou facteur de forme. Il évalue le caractère rectangulaire de la courbe $I (V)$ . Il varie de 0.25 pour une cellule à faible rendement à 0.9 pour une cellule idéale.

Il varie de 0.25 pour une cellule à faible rendement à 0.9 pour une cellule idéale.

Définition : Rendement

Le rendement d'une photopile est donné par le rapport entre la puissance maximum débitée et la puissance du rayonnement incident.

η = \frac{V_{m} I_{m}}{P_{solaire}} = \frac{FF V_{CO} I_{CC}}{P_{solaire}}

Remarque :

L'expression montre que les performances d'une photopile ne dépendent que des valeurs des trois paramètres.

Ces paramètres sont fonction d'une part de propriétés spécifiques du matériau et d'autre part de paramètres technologiques.

Propriétés spécifiques : le gap, les coefficients d'absorption et de réflexion, la longueur de diffusion des porteurs, la vitesse de recombinaison en surface.

Paramètres technologiques : la profondeur de la jonction, la largeur de la zone de charge d'espace, la présence de résistances parasites.

Attention : Modèle équivalent

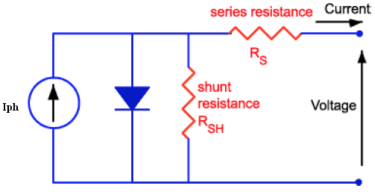
$R_{s}$ et $R_{sh}$ représentent les pertes internes :

$R_{s}$ = résistance série de la diode.
$R_{sh}$ représente le courant de fuite à la jonction : $R_{sh} = \frac{V + R_{s} I}{I_{ph} - I_{s} {\exp [\frac{q (V + R_{s} I)}{kT}] - 1} - I}$

Définition :

Le courant peut s'exprimer sous la forme :

$I = I_{ph} - I_{s} {\exp [\frac{q (V + R_{s} I)}{kT}] - 1} - \frac{V + R_{s} I}{R_{sh}}$ .

Remarque :

On ne peut pas la calculer mais simplement la mesurer. Elle est déterminée au point (0, $I_{CC}$ ).

Les formulations du paramètre $FF$ sont données ci-dessous :

Cas idéal : ${FF}_{0} = \frac{v_{oc} - Ln (v_{oc} + 0,72)}{v_{oc} + 1}$ avec $v_{oc} = \frac{V_{OC}}{n U_{T}} et τ_{s} = \frac{R_{s}}{V_{OC} / J_{ph}}$ .
Avec $R_{s}$ et sans $R_{sh}$ : ${FF}_{s} = {FF}_{0} (1 - 1,1 R_{s}) + \frac{R_{s}^{2}}{5,4}$
Avec $R_{s}$ et $R_{sh}$ : $FF = {FF}_{s} (1 - \frac{v_{oc} + 0,7}{v_{oc}} \frac{{FF}_{S}}{R_{sh}})$

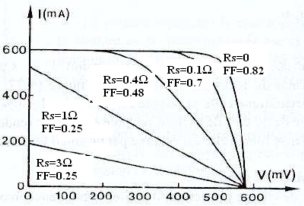
Effet de la résistance série

Si $V_{j}$ est la tension aux bornes de la jonction, on a :

I = I_{ph} - I_{s} {\exp [\frac{q V_{j}}{kT}] - 1}, V = V_{j} - R_{s} I, I = I_{ph} - I_{s} {\exp [\frac{q (V + R_{s} I)}{kT}] - 1},

Les courbes ci-dessous montrent les effets de $R_{s}$ sur le facteur de forme ( $FF > 0,8$ pour $R_{s} = 0$ et $FF = 0,25$ pour $R_{s} > 1 Ω$ ). Pour $R_{s} = 0$ , il passe de 0.83 dans le Si ( $\approx 0,6 V$ ) à 0.87 dans le GaAs ( $\approx 0,9 V$ ) par exemple.