La photodiode à avalanche (APD)
Définition : Constitution – principe de fonctionnement
Une photodiode à avalanche (APD) transforme, comme son nom l'indique, un photon en une cascade de paires électron-trou selon le phénomène d'avalanche qui régit les jonctions faiblement dopées et fortement polarisées en inverse. Ainsi, une lumière faible peu produire un courant suffisamment élevé pour être détecté par l'électronique de lecture en aval de l'APD. Une APD est donc constituée comme une PIN mais elle est polarisée dans sa zone d'avalanche par une très forte tension inverse. pour une APD au silicium. La zone de multiplication ou se produit le phénomène d'avalanche se fait dans une grande zone I entièrement dépeuplée
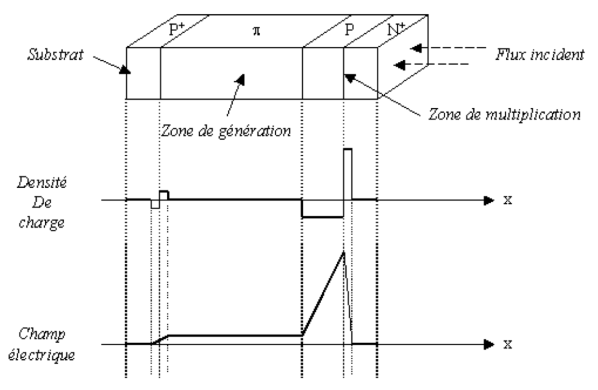
La photodiode à avalanche fonctionne donc avec une forte tension de polarisation inverse de façon à ce que son point de fonctionnement soit très proche du régime de claquage.
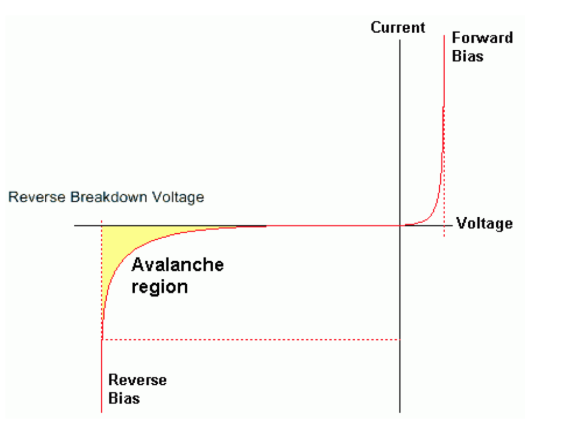
La capacité des porteurs à réaliser des ionisations par impact est caractérisée par les coefficients d'ionisation et pour les électrons et les trous respectivement. Ces quantités représentent les probabilités d'ionisation par unité de longueur . et augmentent avec le champ électrique dans la zone de charge d'espace (zce[1]), et diminuent avec l'augmentation de la température dans la photodiode (car l'augmentation de la température augmente les collisions donc diminue les chances d'obtenir assez d'énergie cinétique pour générer de nouveaux porteurs). On définit le rapport d'ionisation tel que :
Typiquement, ce rapport d'ionisation est égal à 0,9 pour les APD au Germanium, 0,45 pour les APD au InGaAs et 0.02 pour les APD au Silicium. Les filières Silicium s'avèrent être les meilleures quant à la fabrication des APD, car plus le rapport d'ionisation est faible, meilleures sont les performances en termes de temps de réponse, de bruit et de gain. En effet, il n'est pas très bon que soit très proche de 1 car les trous comme les électrons ont la même probabilité de créer de nouveau porteur par ionisation par impact. Les trous créés vont aller dans une direction balayés par le champ électrique interne. Ces derniers vont créer des électrons qui vont aller dans la direction opposée et qui vont à leur tour créer des trous, etc., ce qui peut ne pas avoir de fin. Cela engendre de très grand gain, mais diminue la bande passante du dispositif par un temps de réponse prohibitif. Dans cette configuration, le bruit est également fortement détérioré à cause du caractère fortement aléatoire du processus d'ionisation par impact. On retrouve ce comportement dans les abaques de McIntyre qui prédisent la densité spectrale de bruit en fonction du gain et des coefficients d'ionisation des porteurs. Ainsi, lorsque tend vers 0, un seul type de porteur, les électrons en l'occurrence, ont une très grande probabilité de créer de nouvelles paires électron-trou. Le temps du processus de multiplication par l'ionisation par impact est donc limité et s'arrête lorsque le dernier électron quitte la zone de multiplication. En contrepartie, le gain est lui aussi limité par cette configuration.
Définition :
Le courant de détection disponible en sortie de l'APD dépend du gain , de la sensibilité spectrale de l'APD et de la puissance optique incidente :
Le photocourant primaire hors multiplication par le phénomène d'avalanche Iprim, est le même que celui émis par une photodiode PIN, soit :
Le gain photoélectrique interne est donné par la relation de Miller. représente la valeur absolue de la tension de claquage de la jonction, la valeur absolue de la tension inverse de polarisation et l'indice de concavité de la zone d'avalanche défini de façon empirique (égal à 5 dans des conditions de quasi obscurité) :