I.2 Diagrammes d'énergie

Reprenons les deux matériaux précédents et raisonnons maintenant en terme de diagrammes d'énergie. Ils peuvent, pour des matériaux dopés, se représenter suivant la figure ci-dessous, dans le cas ou les matériaux sont isolés.

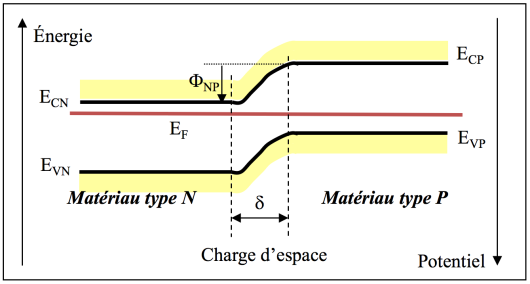
Pour un matériau de type N, les électrons étant majoritaires, le niveau de Fermi se situe près de la bande de conduction alors que pour un type P où ce sont les trous qui sont majoritaires, il se situe près de la bande de valence.

Si nous mettons ces deux matériaux en contact, la seule constante qui va exister dans ce système sera le niveau de Fermi. Le diagramme de bandes va donc évoluer de manière à ce que les niveaux de Fermi de chaque constituant s'alignent, engendrant, par conséquent, une déformation des bandes d'énergie.

Loin de la jonction métallurgique, on va retrouver les matériaux originels ; par contre, au voisinage de celle ci, il va y avoir courbure des bandes car leur variation ne peut être que continue: Le passage de la région N à la région P se fait graduellement, sans discontinuité.

La courbure des bandes d'énergie fait apparaître une barrière de potentiel (due à l'existence d'un champ électrique) qui va s'opposer au passage des porteurs des régions où ils sont en forte concentration vers les régions où ils sont en faible concentration.

Il existe donc deux phénomènes antagonistes:

  • Un phénomène de diffusion dû au gradient de concentration,

  • Un phénomène de conduction dû à l'apparition d'un champ électrique induit par la diffusion.

Fondamental

La zone centrale appelée « charge d'espace » est une zone dans laquelle règne un champ électrique important (plusieurs kilovolts par centimètre) et sera donc dépourvue de porteurs libres. Elle se caractérise par sa hauteur Φ NP %iPHI_{ NP } et sa largeur δ %delta .

Nous allons dans ce qui suit déterminer les équations permettant de calculer ces deux éléments caractéristiques.

Définition

La différence de potentiel est assimilable à une différence d'énergie telle que:

Φ NP = Φ N − Φ P = − 1 q ( E CN − E CP ) = = − 1 q ( E VN − E VP ) %iPHI_{ NP }= %iPHI_{ N}- %iPHI_{ P }= - { 1 over q } ( E_{CN}-E_{CP} ) = `= - { 1 over q } ( E_{VN}-E_{VP} )

On l'appelle « hauteur de barrière » ou « barrière de potentiel ». On peut aussi dire « barrière de diffusion » lorsque la jonction n'est pas polarisée.