L'état cristallin
1 La géométrie du réseau cristallin
Un cristal est construit à partir de n atomes constituant la base, la base étant répétée périodiquement suivant 3 vecteurs fondamentaux appelés vecteurs primitifs.
Rq.: la base est parfois appelée motif.
Ayant choisi dans un cristal une origine quelconque O, on retrouve en tout point A du cristal tel que :
n1, n2, n3 entiers quelconques, le même environnement atomique qu'au point O.
L'ensemble des points A définis à partir de O constitue un réseau géométrique de points.
Les points A sont les nœuds du réseau.
Le parallélépipède construit sur les 3 vecteurs fondamentaux est une maille cristalline.
A chaque réseau correspond donc plusieurs mailles. On appelle maille élémentaire la maille pour laquelle les longueurs a, b, c sont minimales.
Elle ne contient qu'1 nœud en propre pour quelques corps simples.
C'est un parallélépipède dont les sommets sont les 8 nœuds correspondants aux 8 mailles adjacentes.
Il est parfois avantageux, pour décrire un cristal, de considérer une maille plus grande que la maille élémentaire.
Prenons l'exemple d'une maille élémentaire rhomboédrique, c'est-à-dire bâtie sur 3 vecteurs égaux et formant entre eux des angles de 60°.
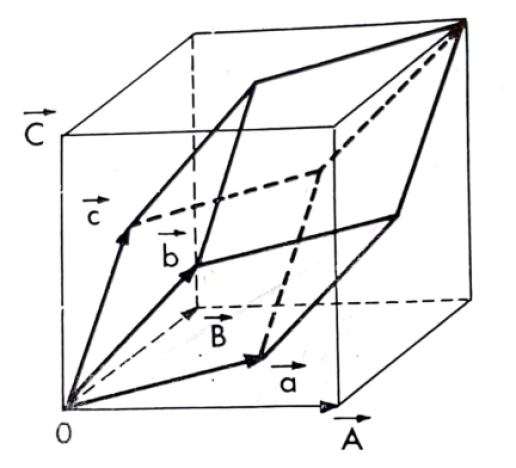
Plutôt que cette maille élémentaire, il est plus aisé de considérer la maille bâtie sur 3 vecteurs définis par :
Ces 3 vecteurs sont égaux de longueur
Fondamental :
La maille correspondante est cubique, elle a un nœud en chaque sommet et au milieu de chaque face. Elle est dite Cubique à Faces Centrées (CFC).
La maille cubique possède 4 nœuds en propre (voir calcul ) alors que la maille rhomboédrique n'en a qu'un seul. La maille cubique est donc 4 fois plus volumineuse que la maille élémentaire.
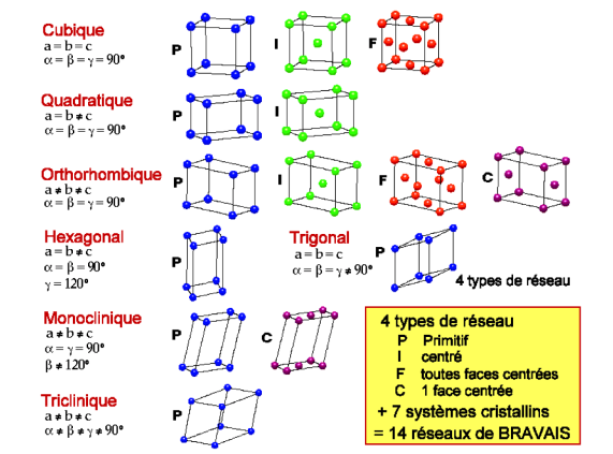
2 Les systèmes cristallins
Une maille quelle qu'elle soit et par suite un système cristallin est donc caractérisé par les 6 paramètres suivants :
les longueurs a, b, c des 3 vecteurs,
les angles α, β, γ qu'ils font entre eux.
Selon la valeur de ces 6 paramètres, on définit 7 systèmes cristallins.
Parmi ces systèmes, selon la position des nœuds du réseau, on définit 14 réseaux de Bravais