Equation du viriel empirique : expression en densité et en pression
Définition : Equation du viriel en densité
En résumé de l'intéressante revue historique sur l'équation du Viriel publiée dans Mason_Spurling, 1969[1], Kamerlingh Onnes a proposé en 1901 deux expressions théoriques dont la deuxième est une expansion infinie de la pression en série de la densité molaireρ :
où la "densité molaire" (terme emprunté aux anglo-saxons) est l'inverse du volume molaire : ρ = N / V
propriétés :
le terme de gauche est appelé facteur de compressibilité Z= PV/RT (à ne pas confondre avec ZN, la fonction de partition dans l'ensemble canonique) :
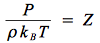
La troncature au premier terme "1" conduit à l'équation des gaz parfaits.
Les coefficients du viriel dépendent de la température et de la nature du fluide, mais ni de la densité, ni de la pression.
Les autres termes sont des corrections provenant de imperfections au sein du fluide, notamment dues aux interactions entre particules.
le second coefficient du viriel, B dépend des interactions 2 à 2 dans le fluide
le troisième coefficient du viriel, C dépend des interactions 3 à 3 dans le fluide
le quatrième coefficient du viriel, D dépend des interactions 4 à 4 dans le fluide.
etc...
Définition : Equation du viriel en pression
Une écriture alternative de la pression est basée sur une série en pression :
Naturellement, il existe une relation entre les coefficients des deux expressions :
B = RT.B '
C = (RT)2.(C '+B '2)
D = (RT)3.(D ' + 3B ' C '+B '3)
E = (RT)3.(E '+ 4D ' B ' + 6C ' B '2+2C '2+B '4)
...
Remarque : Validité des deux équations en pression et en densité
Seule la série de la densité a une signification théorique avérée : ses coefficients B C D E contiennent tous des termes appelés "viriel". Par conséquent :
Seule la série en densité est appelée équations du viriel.
Il n'est PAS recommandé d'appeler coefficient du viriel les coefficients B' C' D' E' dans la série en pression.
Dans l'usage courant, l'expansion en série de la pression est intéressante :
Fixer C = D = E = .... = 0 revient à ne tenir compte que des interactions 2 à 2 dans le fluide. C'est l'hypothèse courante d'un potentiel d'interaction de paire additif. Mais elle n'est valide que sur une plage de conditions expérimentales limitées.
Fixer C ' = D ' = E ' = .... = 0 revient à tenir compte des interactions 2 à 2 dans le fluide, ET implicitement des interactions 3 à 3 car C ' = 0 impliquent que C est non nul puisque C = (RT)2.(C '+B '2).
