Qualité des données
Plusieurs indicateurs de qualité des données ont été développés :
La fiabilité des données qui découle de la méthode de mesure utilisée et des procédures de vérification
L'exhaustivité qui dépend du nombre d'entreprises considérées sur une période de temps donnée
Les corrélations géographiques, temporelles et technologiques qui indiquent si les données utilisées couvrent le lieu, la période et la technologie du processus étudié
La taille de l'échantillon
Pour chacun de ces indicateurs, des scores allant de 1 (meilleur score) à 5 (score le plus mauvais) peuvent être attribués.
Ce tableau présente les critères permettant d'attribuer les scores.
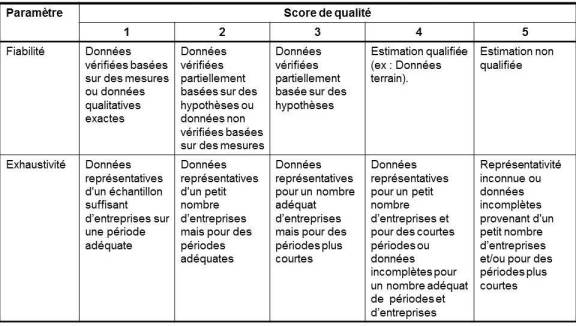

Un facteur d'incertitude peut être attribué à chacun des scores de cette matrice.
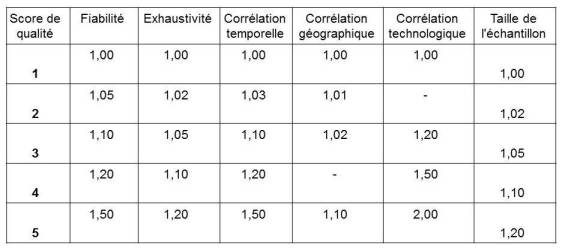
L'évaluation quantitative des données s'appuie sur une table de correspondance entre les différentes notes utilisées lors de l'évaluation qualitative et des facteurs d'incertitude. Ces facteurs d'incertitude permettent ensuite de calculer la variance V 95 (avec un intervalle de confiance de 95%), l'écart-type puis l'incertitude de chacune des données via la formule statistique suivante (Frischknecht, 2007a).

Exemple :
Prenons l'exemple d'un processus nécessitant une certaine quantité d'aluminium (par ex. quantité d'aluminium nécessaire pour la fabrication d'un couvercle de Yogourt). Supposons que les données sur la quantité d'aluminium aient les caractéristiques suivantes :
- Vérifiées et basées sur des mesures (score de qualité 1 pour la fiabilité)
- Représentatives d'un petit nombre d'entreprises et pour la période temporelle adéquate (score de qualité 2 pour l'exhaustivité)
- Obtenues moins de 3 ans avant l'étude voulue (score de corrélation temporelle de 1).
- Provenant d'une zone géographique ayant des conditions légèrement similaires aux conditions de l'étude (score de corrélation géographique de 4).
- Correspondant exactement au type d'aluminium voulu (score de corrélation technologique de 1).
- Obtenues à partir d'un échantillon de taille inconnue (score de qualité pour la taille de l'échantillon de 5)
La variance de la quantité d'aluminium est alors de 1,21. Une fois l'incertitude sur une donnée individuelle déterminée, ces incertitudes individuelles sont ensuite combinées avec les données d'autres processus unitaires à l'aide de méthode statistiques (du type Monte-Carlo).






