Numerical methods
Numerical methods
leads to an incremental least squares problem
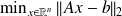 (
(
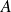 is a several
is a several
 dense matrix)
dense matrix)can be solved by :
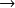 normal equations method (
normal equations method (
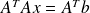 )
)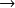 or orthogonal transformations (e.g QR)
or orthogonal transformations (e.g QR)requirements :
 Performance (daily computation)
Performance (daily computation) Memory storage
Memory storage
Normal equations
steps for solving
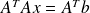 :
:updating
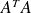 (
(
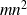 flops)
flops)Cholesky factorization
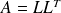 (
(
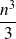 flops)
flops)triangular solve :
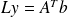 followed by
followed by
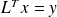 (
(
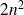 flops)
flops)
computational cost:
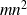 flops (if
flops (if
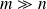 )
)accuracy:
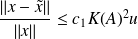
QR factorization
general QR :
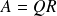 with
with
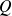
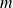 -by-
-by-
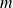 orthogonal and
orthogonal and
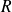
 -by-
-by-
 upper triangular, compute
upper triangular, compute
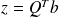 , and solve
, and solve
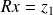 (
(
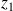 denotes the first $
denotes the first $
 $ elements of
$ elements of
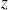 )
)incremental QR :
only
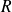 is stored and updated
is stored and updatedwe perform
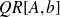
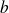 is overwritten by
is overwritten by
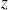
computational cost:
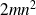 flops (if
flops (if
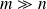 )
)accuracy:
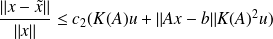
Normal equations vs QR factorization
QR costs twice (
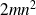 vs
vs
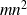 )
)by forming the normal equations we square the condition number
if
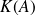 is large and the residual is small then the normal equations may be less accurate
is large and the residual is small then the normal equations may be less accuratewhen applied to large residual, ill-conditioned problems, we get comparably inaccurate results
Need for parallelism
Supposing that peak performance of matrix-matrix product: 4.2 Gflops then
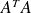 (or
(or
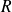 ) in-core
) in-core
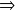
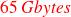 impossible with 32 procs and 2Gbytes memory per proc
impossible with 32 procs and 2Gbytes memory per procassembling time (sequential)
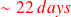
result within a day using 32 procs depends on scalability of the algorithm
Existing libraries
Standard parallel libraries for dense linear algebra computations on parallel distributed machines:
ScaLAPACK (University of Tennessee - J. Dongarra)
PLAPACK (University of Texas, Austin - R. Van de Geijn)
There is no packed format for symmetric (ATA) or triangular (R) matrices in ScaLAPACK or PLAPACK (the
whole matrix is stored)
Objectives
exploit parallelism
take profit of the structure by storing half of the matrix (32.5 Gbytes instead of 65 Gbytes),
obtain Gflops performance similar to ScaLAPACK





