Définitions et propriétés
Introduction
Soient 
et 
deux espaces vectoriels sur le même corps 
, de dimensions finies respectives 
et 
. Du point de vue des applications linéaires, la transposition est une opération particulière qui, à une application 
(représentée par la matrice
), associe une application 
(représentée par la matrice
).
Définition :
La transposée d'une matrice
, notée
, est définie par :
avec 
Le résultat étant cette fois dans 
. Du point de vue purement matriciel, les lignes de la matrice
deviennent les colonnes de la transposée .
Exemple :
.
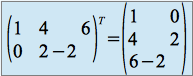Fondamental : Propriété
La transposition est elle même une application linéaire de l'espace des matrices 
dans l'espace des matrices , c'est à dire un élément de 
.
