Introduction par un exemple
Exemple :
Soit 
une application linéaire de 
, de base canonique 
, dans 
, de base canonique 
.
DANS LES BASES CANONIQUES,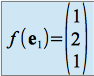 
, 
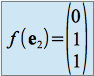et a pour matrice :
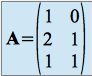
Introduisons deux nouvelles bases :
de , et 
de .
Déterminons alors la matrice
de dans ces nouvelles bases. Il suffit, pour cela, de trouver les coordonnées de 
et 
dans la base 
.
On exprime, tout d'abord, dans la base , on obtient :
car est linéaire. Ainsi,
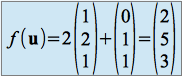
ce qui peut aussi s'écrire
.
De même dans la base , a pour coordonnées
.
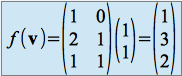Il faut, ensuite, exprimer et dans la base . Pour cela, il faut exprimeren fonction de .
On a :
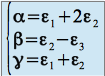
d'où on obtient:
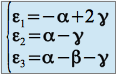
Enfin, après calcul, on peut écrire :
et la nouvelle matrice de dans ces nouvelles bases est :
On dit que les matrices
et
sont équivalentes. Cela signifie qu'elles représentent la même application linéaire dans des bases différentes.
