Mise en équation du bilan thermique
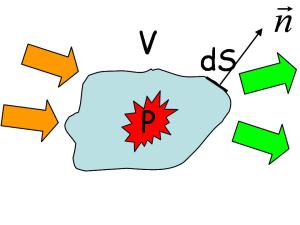
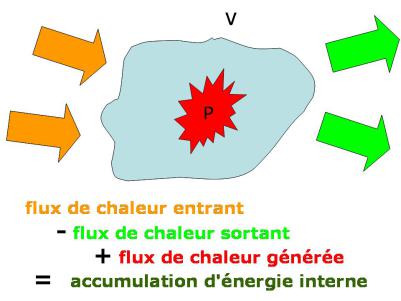
Ecrivons la conservation de l'énergie thermique dans un élément de volume de solide quelconque V (figure 3) :
La chaleur entre dans l'élément et en sort par conduction. On définit le vecteur normal unitaire orienté vers l'extérieur (figure 4). Alors :
|  Figure 4 |
Remarque :
Le signe moins est dû au fait que la normale est dirigée vers l'extérieur et que, par convention, tout ce qui entre dans le volume V est compté positivement.
P est la puissance générée (au sens large) par unité de volume en J.s-1.m-3. Elle peut être générée dans l'élément par dégradation d'énergie électrique (effet joule), par fission ou comme le résultat d'une réaction chimique. Alors :
Flux de chaleur générée = ± |
Il est compté positivement si il génère de l'énergie et négativement si il en consomme.
Si U représente l'énergie interne par unité de masse, on peut écrire :
Accumulation d'énergie interne : |
Dans le cas d'un solide, l'énergie interne par unité de masse U s'écrit :
|
Le bilan de conservation de l'énergie thermique devient alors :
±
= 
.......................................................(équation 25)
En transformant l'intégrale de surface en intégrale de volume (théorème de GREEN-OSTROGRADSKI) et en revenant à l'élément différentiel, on écrit alors :
- div |
Complément : Démonstration du théorème de GREEN-OSTROGRADSKI
Dans l'équation générale que nous venons de démontrer, 
est la densité de flux thermique, par conduction dans le cas de solides, qui s'exprime par la loi de Fourier :
|
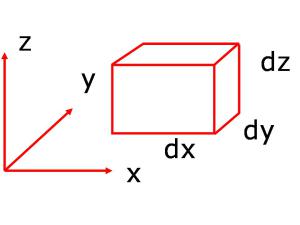
Ces équations seront écrites dans les configurations géométriques habituelles, en utilisant les expressions des div et grad adaptées.
Dans le cas d'un système cartésien tridimensionnel (figure 5), les équations ci-dessus conduisent à :
|  Figure 5 |
